Statistisch model kankerdiagnoses

De ‘verwachte’ incidentie van een postcodegebied

De data die beschreven staan onder data over kanker en populatie zijn gebruikt om voor elk gebied in Nederland met behulp van statistische modellen zogenaamde gestandaardiseerde incidentie ratios (‘Standardized Incidence Ratios’ [SIR]) te schatten. 

De SIR is de ratio van het aantal waargenomen kankerdiagnoses in een gebied en het aantal kankerdiagnoses dat verwacht wordt in dat gebied. Het verwachte aantal kankerdiagnoses is het aantal diagnoses dat je verwacht in een gebied als het risico op kanker overal in Nederland gelijk zou zijn. Hierbij moeten we rekening houden met het aantal mensen dat in een gebied woont en hoe oud ze zijn. In een dichtbevolkt gebied komt namelijk meer kanker voor dan in een dunbevolkt gebied, net als dat in een gebied met relatief meer ouderen meer kanker voor zal komen dan in een gebied met meer jongeren. Deze effecten van verschillen in leeftijd en populatiegrootte moeten niet meer zichtbaar zijn in de uiteindelijke atlas. 

Om de SIR te berekenen moet eerst wordt berekend hoeveel kankerdiagnoses er gemiddeld worden gesteld in Nederland per leeftijdscategorie en per persoon (of per 100.000 personen). Dat noemen we het zogenaamde leeftijdsspecifieke incidentiecijfer. Als het risico in Nederland overal gelijk is, verwachten we dat het leeftijdsspecifieke incidentiecijfer in ieder gebied ongeveer hetzelfde is. Als we weten hoeveel mensen van welke leeftijd er in een gebied wonen, kunnen we terugrekenen hoeveel kankerdiagnoses we verwachten in dat gebied als de gemiddelde leeftijdsspecifieke incidentiecijfers in dat gebied hetzelfde zijn als die van Nederland. We vermenigvuldigen daarvoor per leeftijdscategorie het Nederlandse leeftijdsspecifieke incidentiecijfer met het aantal mensen dat in het gebied woont. Door daarna het aantal verwachte kankerdiagnoses per leeftijdscategorie op te tellen krijgen we het totale absolute aantal verwachte kankerdiagnoses in dat gebied. In formule ziet dit er als volgt uit: 

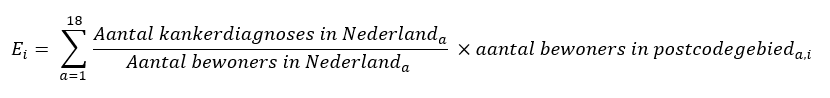
Hierin is E_i het verwachte aantal kankerdiagnoses in gebied i. a staat voor de leeftijdscategorie: leeftijdscategorie 1 bevat de leeftijden 0-5 en leeftijdscategorie 18 de leeftijden 85 en ouder. Deze berekening is een vorm van indirecte standaardisatie. Dit zorgt ervoor dat verschillen tussen gebieden niet toe te schrijven zijn aan een oudere of jongere bevolking in die gebieden en ook niet aan verschillen in populatiegrootte tussen gebieden. 

Vervolgens wordt de waargenomen incidentie in dit gebied vergeleken met de verwachte incidentie. Dit vergt een statistisch model. 

(On)zekerheid rondom incidentie – Gebieden met weinig inwoners

Door de waargenomen incidentie (aantal nieuwe kankerdiagnoses) in elk gebied te vergelijken met de verwachte incidentie, berekenen we of dit gebied een hogere of lagere incidentie heeft dan we zouden verwachten op basis van het Nederlandse gemiddelde en de populatiegrootte en leeftijdsverdeling van het specifieke gebied. 

Echter, niet ieder gebied bevat evenveel inwoners en evenveel kankerdiagnoses en vooral gebieden met lage aantallen inwoners en/of weinig kankerdiagnoses kunnen een vertekend beeld geven en de onderliggende geografische patronen vertroebelen. De kankerincidentie in gebieden met weinig inwoners en/of een weinig kankerdiagnoses is namelijk sterker onderhevig aan willekeurige veranderingen dan gebieden met meer inwoners of een hogere incidentie. Een verschil van 1 kankerdiagnose pakt in een gebied met een lage incidentie veel extremer uit dan een verschil van 1 kankerdiagnose in een gebied met een hoge incidentie. 

In een hypothetisch en versimpeld voorbeeld: Als in een klein gebied 3 kankerdiagnoses worden waargenomen en er worden er 2 verwacht (SIR= 3/2 = 1.5), dan lijkt de incidentie 50% hoger dan verwacht. Maar in een groter gebied waar 30 kankerdiagnoses worden waargenomen en er 29 worden verwacht (SIR = 30/29 = 1.03) is de incidentie slechts 3% hoger dan verwacht. Kleine gebieden kunnen op deze manier voor extreme uitschieters zorgen, terwijl de verschillen soms simpelweg door willekeur komen.

Door te ‘smoothen’ ontstaan stabielere schattingen van de SIR. Daarnaast is het zo dat de onzekerheid rondom een geschatte SIR vaak groter is in gebieden waar weinig mensen wonen en/of weinig kanker voorkomt. Dat komt doordat er minder data beschikbaar zijn om de schatting van de SIR op te baseren. Door te ‘smoothen’ wordt niet alleen de geschatte SIR stabieler, maar ook de onzekerheid rondom de geschatte SIR vaak kleiner. In het algemeen zorgt ‘smoothing’ er dus voor dat de extreme uitschieters minder extreem worden en de onzekerheid ervan kleiner wordt. Dit leidt tot een stabieler en realistischer beeld van het geografische patroon van de kankerincidentie. 

Zie figuur 7a voor een voorbeeld van hoe smoothing werkt.

Figuur 7a. Links: geobserveerde incidentie. Rechts: incidentie met smoothing.

Voor de Nederlandse Kankeratlas volgen we de methodologie die gebruikt is voor de Australische Kankeratlas, en gebruiken we een Bayesiaans model met een Conditional Autoregressive (CAR) Distribution.

Figuur 7a. Links: geobserveerde incidentie. Rechts: incidentie met smoothing.

In de Nederlandse Kankeratlas volgen we de Australische Kankeratlas, en gebruiken we een Bayesiaans model met een Conditional Autoregressive (CAR) Distribution.

Statistische modelspecificatie

We veronderstellen dat de geobserveerde incidentie (aantal kankerdiagnoses) Yi in gebied i een Poissonverdeling (een bepaalde kansverdeling) volgt:

Waar E i  het verwachte aantal kankerdiagnoses  het natuurlijk logaritme van de zogenaamde Standardized Incidence Ratio (SIR) is in gebied i. Geëxponentieerd geeft de waarde  aan in welke mate een gebied afwijkt van het gemiddelde: een SIR van 1 geeft aan dat een gebied een incidentie heeft die gelijk is aan wat zou worden verwacht volgens het Nederlandse gemiddelde (). Een SIR onder de 1 geeft aan dat een gebied een lagere incidentie heeft dan verwacht zou worden op basis van het Nederlandse gemiddelde en een SIR hoger dan 1 een hogere incidentie dan verwacht.

Deze SIR-waarden, in combinatie met hun onzekerheid, worden getoond in de Nederlandse Kankeratlas. Het logaritme van de SIR wordt vervolgens geparametriseerd als:

De parameter  staat voor de gemiddelde SIR, en  staat bekend als een ruimtelijk ‘random effect’ en vertegenwoordigt de mate waarin gebied i afwijkt van dit gemiddelde. De specificatie van deze ruimtelijke random effects bepaalt hoe smoothing wordt uitgevoerd. In Bayesiaanse modellen worden eerst ‘priors’ gespecificeerd, ook wel a-priori verdelingen genoemd. Dit is onze mate van kennis voordat de data verwerkt zijn. Die kennis wordt vervolgens aangepast zodra het model de data verwerkt en dat leidt tot een a-posteriori verdeling. De a-priori verdeling voor    is normaal verdeeld met een gemiddelde van 0 (want , ofwel gemiddeld zullen gebieden overeenkomen met het Nederlandse gemiddelde) en met een heel brede variantie; dit laatste betekent dat we vooraf weinig over de data willen aannemen en daarmee dat de data veel invloed kunnen hebben op onze uiteindelijke schatting;

De ruimtelijke random effects  volgen een verdeling zoals voorgesteld door Leroux et al. 2000; deze waarden zijn een gewogen gemiddelde waarin ook de waarden van random effects van buurgebieden worden meegenomen. Op deze wijze vindt de eerder genoemde ‘smoothing’ plaats;

Vervolgens hebben ook , en een zogenaamde ‘a-priori verdeling’, die vervolgens met behulp van de geobserveerde data preciezer geschat kan worden. De a-priori verdeling voor  volgt een inverse gamma distributie met vormparameter 1 en schaalparameter 0.01:

Ook hier betekent een schaalparameter van 0.01 dat we vooraf zeer weinig aannemen over de waarden, en daarmee zeer veel gewicht geven aan de geobserveerde data. Als laatste is de a-priori verdeling voor ;

Een van 0 zou betekenen dat er geen ruimtelijke correlatie is (elk gebied is onafhankelijk van haar buurgebieden), en een van 1 zou volledige afhankelijke relatie betekenen. Door een uniforme distributie van 0 tot 1 aan te nemen, is elke mogelijke waarde tussen 0 en 1 mogelijk; ook hier heeft de data daarom een sterke invloed op de schatting.

Referenties

Leroux BG, Lei X, Breslow N. Estimation of disease rates in small areas: a new mixed model for spatial dependence. 2000. 135-178. In Halloran ME, Berry D (Eds). Statistical models in epidemiology, the environment and clinical trials. New York: Springer.